

3 : 5 : 7 비율을 갖는 삼각형의 각도Math2024. 1. 4. 17:59
Table of Contents
반응형
흔히

그런데 혹시

코사인법칙을 이용하면 길이가

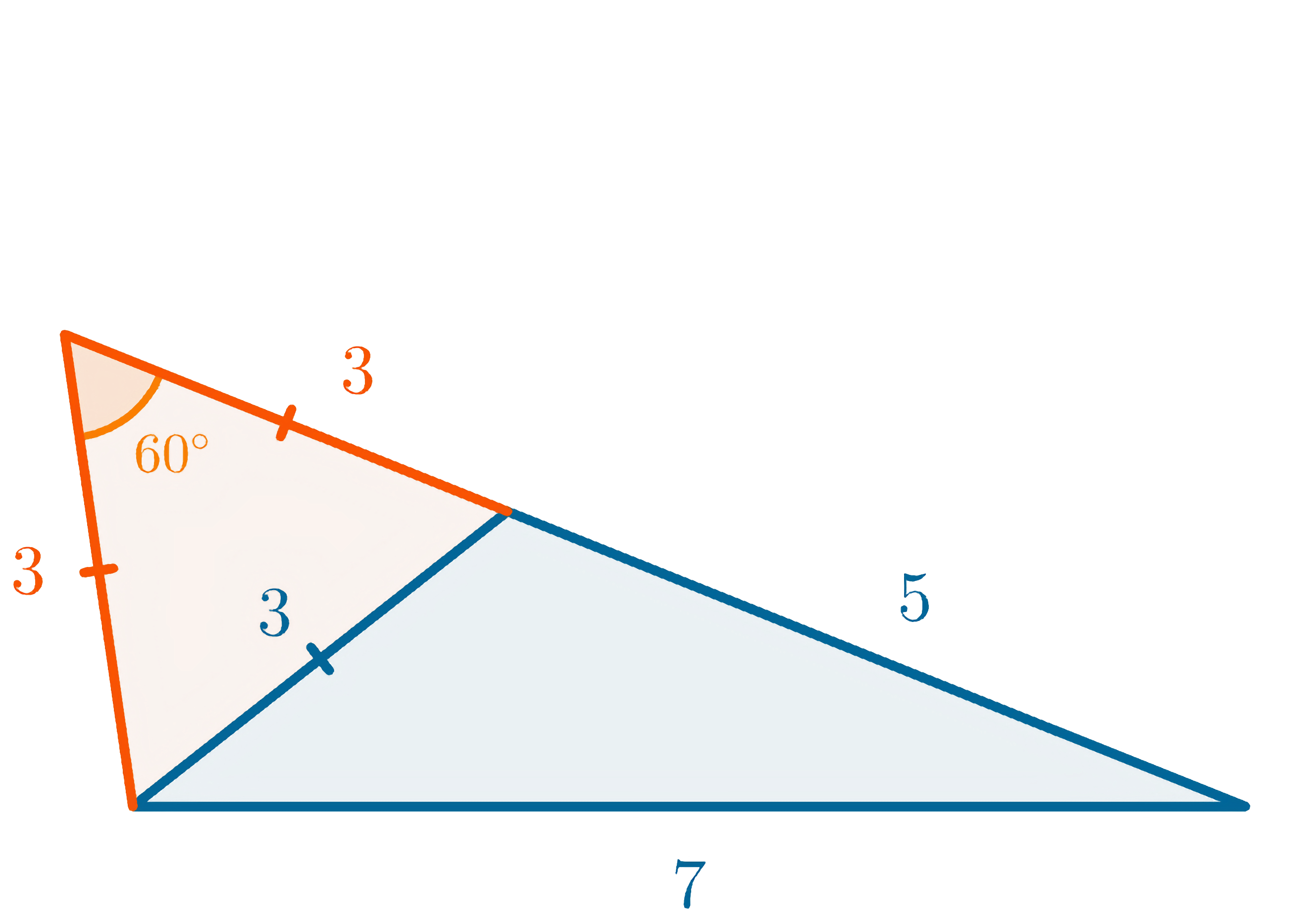
이를 이용하면 길이가
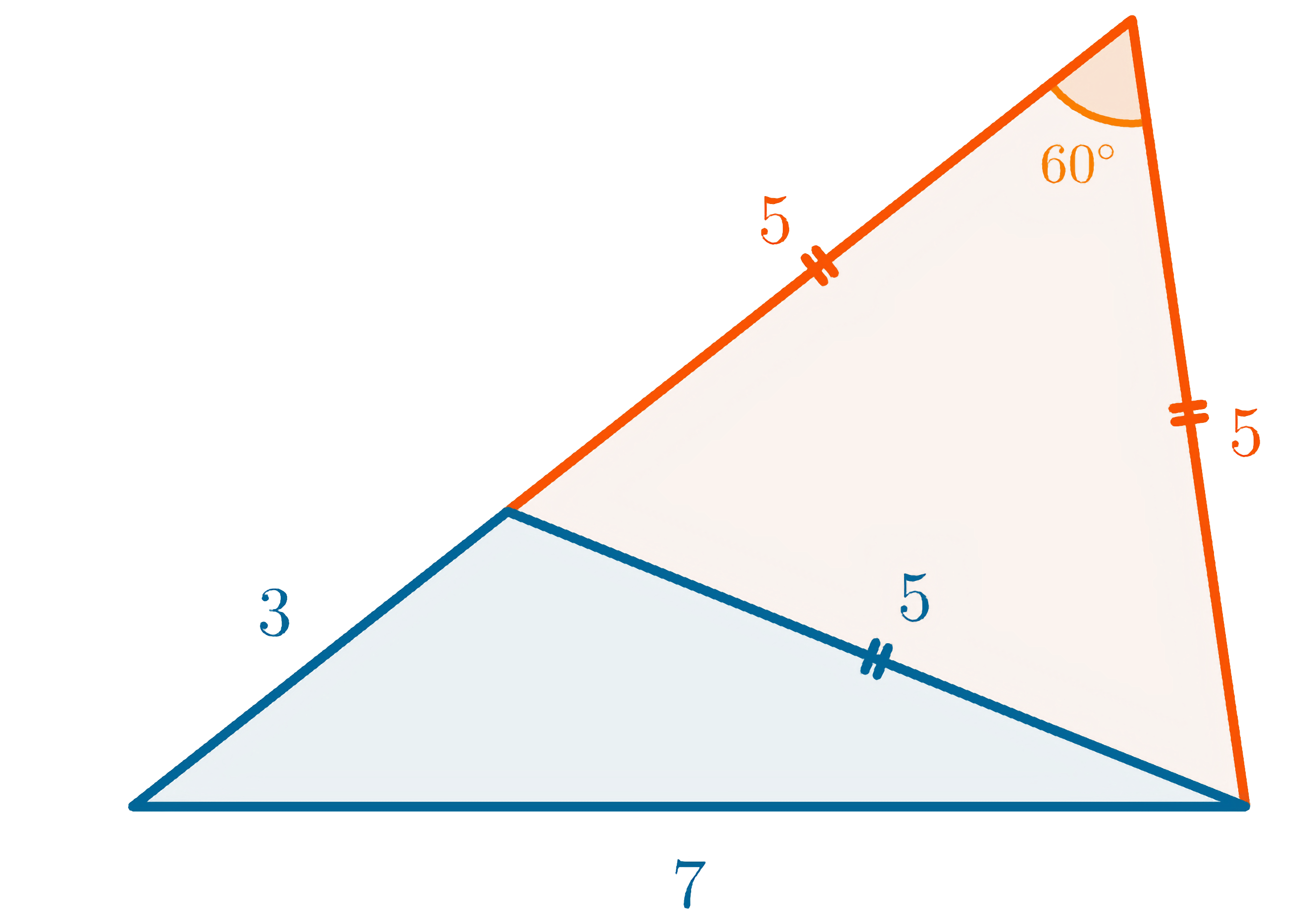
반응형

@Ray 수학 :: Ray 수학
You know what's cooler than magic? Math.
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!



