가산 쐐기합과 하와이언 이어링

import numpy as np
import matplotlib.pyplot as plt

def draw_circle(ax, center, radius, num_points=600):
    t = np.linspace(0, 2*np.pi, num_points)
    x = center[0] + radius*np.cos(t)
    y = center[1] + radius*np.sin(t)
    ax.plot(x, y, linewidth=1.0)

# Model A: Countable wedge of circles as nested circles tangent at the origin,
# with radii increasing (so no entire circle lies in a small neighborhood of the basepoint).
fig1, ax1 = plt.subplots(figsize=(6,6))
N = 12
for n in range(1, N+1):
    R = float(n)            # radius
    C = (R, 0.0)            # center on x-axis so each circle is tangent at (0,0)
    draw_circle(ax1, C, R)
ax1.plot([0], [0], marker='o', markersize=5)  # basepoint
ax1.set_aspect('equal', adjustable='box')
ax1.set_xlim(-1.5, N+1.5)
ax1.set_ylim(-(N+1.5)/2, (N+1.5)/2)
ax1.axis('off')
fig1.tight_layout()
fig1.savefig('/mnt/data/wedge_nested_increasing.png', dpi=220)
plt.show()

# Model B (for contrast): Hawaiian earring (radii decreasing to 0), shown again.
fig2, ax2 = plt.subplots(figsize=(6,6))
M = 40
for n in range(1, M+1):
    r = 1.0/n
    c = (1.0/n, 0.0)
    draw_circle(ax2, c, r)
ax2.plot([0], [0], marker='o', markersize=5)
ax2.set_aspect('equal', adjustable='box')
ax2.set_xlim(-0.1, 2.1)
ax2.set_ylim(-1.2, 1.2)
ax2.axis('off')
fig2.tight_layout()
fig2.savefig('/mnt/data/hawaiian_earring_contrast.png', dpi=220)
plt.show()

print("Saved files:")
print("/mnt/data/wedge_nested_increasing.png")
print("/mnt/data/hawaiian_earring_contrast.png")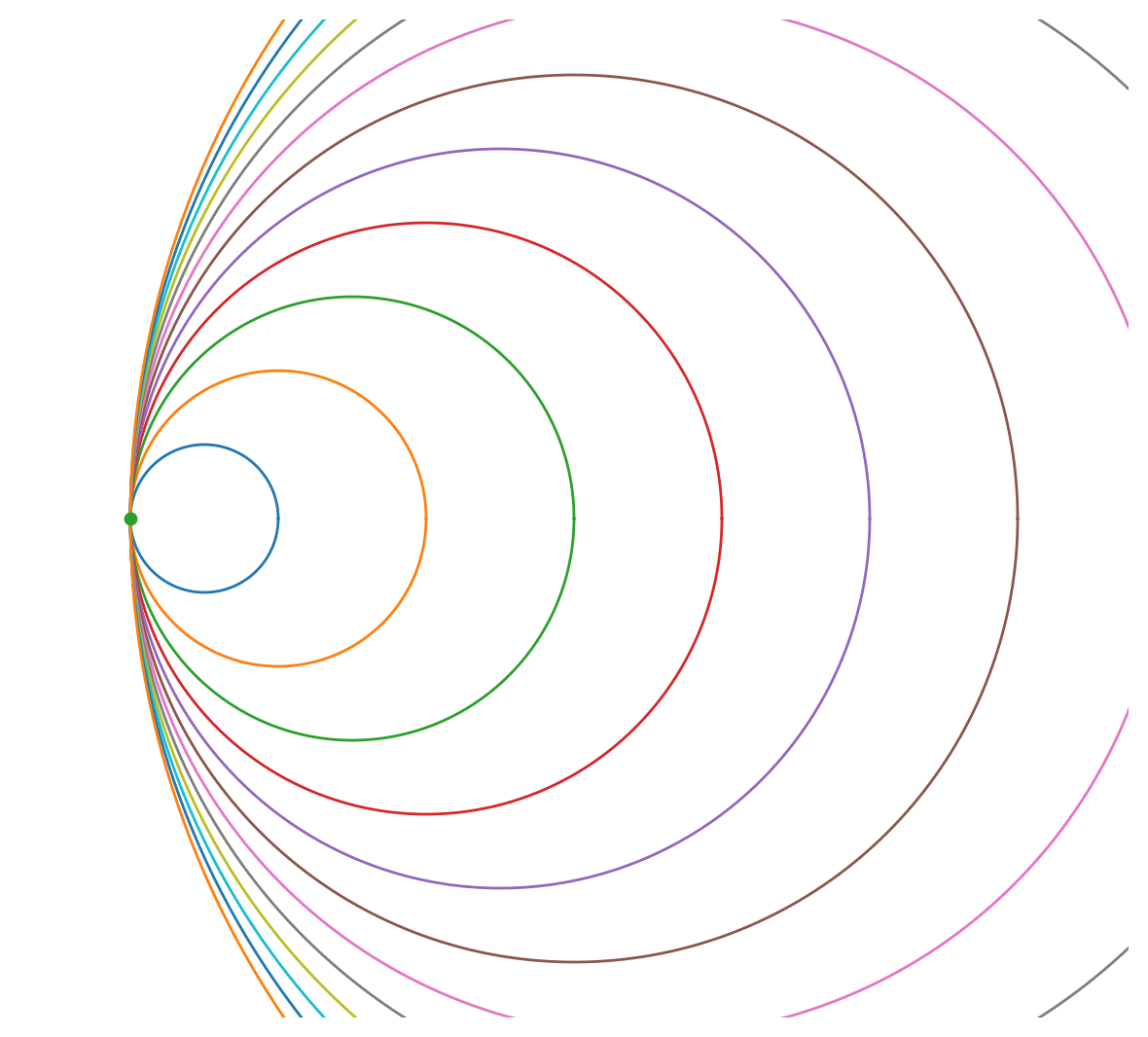

가산 쐐기합 $\displaystyle \bigvee_{n=1}^{\infty} S^1$은 한 점의 동치화(one–point union) 로 얻는 추상적 위상공간 이며, 도형적 배치는 임의다. 다음이 핵심이다.

• 각 성분이 $S^1$과 위상동형 이고,
• 공통 기저점 에서만 만나며(그 밖의 교차 없음),
• 평면에 임베딩했을 때의 부분공간 위상 이 쐐기합의 몫위상(quotient topology) 과 동형이 되도록 만들 수 있다.

이에 따라 “작은 원들이 축적되는 하와이언 이어링(Hawaiian earring)”과 달리, 반경이 커지는 서로 내접(또는 외접)하는 원들 을 택해 원점에서만 접하도록 하면, 어느 작은 근방에도 전체 원 하나가 통째로 들어오지 않으므로 하와이언 이어링과 다른 위상을 갖는다. 이 모델은 가산 쐐기합의 합법적 실현이다.

• 하와이언 이어링: 반지름 $r_n=\tfrac{1}{n}\to 0$. 원점의 임의의 열린 근방이 결국 무한히 많은 “완전한 원” 을 포함하므로 반국소 단일연결이 실패한다.
• 가산 쐐기합의 “커지는 원” 모델: 반지름 $R_n\to \infty$ 등으로 잡아 원점에서만 접하게 하면, 임의의 작은 근방은 각 원의 작은 호(segment) 만 포함하고 전체 원은 포함하지 않는다. 

 

성질	가산 쐐기합 $\bigvee_{n=1}^\infty S^1$	하와이언 이어링 $H$
정의	원 $S^1$들의 한 점에서의 쐐기합(wedge sum). 추상적 몫위상으로 정의됨.	평면 위에서 반지름 $1/n$, 중심 $(1/n,0)$인 원들의 합집합. 부분공간 위상.
컴팩트성	비컴팩트. (무한 개의 원들이 “멀리까지” 퍼져 있으며, 닫히지도 유계하지도 않음.)	컴팩트. (각 원이 유계이고 원점에서 축적되어 닫힘.)
경로 연결성	경로 연결. (모든 원이 기저점에서 연결됨.)	경로 연결. (모든 원이 원점에서 연결됨.)
국소 경로 연결성	성립. (원점 이웃도 항상 유한 개의 원의 작은 호만 포함.)	성립. (평면의 부분공간 위상.)
반국소 단일 연결성	성립. (작은 이웃에서 생긴 고리는 전역적으로 수축 가능.)	불성립. (임의의 작은 이웃에 무한히 많은 원 전체가 포함 → 비자명한 고리들이 남음.)
기본군 $\pi_1$	자유군 $F_\infty$ (가산 개 생성자).	매우 복잡하고 자유군 아님. 비가산적(un-countable), 잘 다루어지지 않는 구조.
보편 덮개	존재. (자유군 $F_\infty$에 대응하는 Cayley graph 같은 구조.)	존재하지 않음.
국소 컴팩트성	불성립. (원점 근방에서 이웃은 무한히 많은 원 부분을 포함하여 상대적 폐집합이 아님.)	성립. (평면의 부분공간이라 각 점은 컴팩트 근방을 가짐.)
컴팩트 생성 여부	컴팩트 생성 공간이 아님.	컴팩트 공간이므로 컴팩트 생성.

---