Synthetic division is a powerful tool in polynomial division, and it is widely used by mathematicians, engineers, and computer scientists. The method is based on the Remainder Theorem and the Factor Theorem and it is used to simplify complex polynomial division problems and obtain accurate solutions. In this comprehensive guide, we will discuss the definitions, theorems, properties, examples, ap..

Biography Euclid of Alexandria, born around 365 BC, was a Greek mathematician, often referred to as the "Father of Geometry." Not much is known about his personal life, including his birth and death dates, but his contributions to mathematics have made him a well-known figure throughout history. Career and Achievements Euclid is most famous for his textbook "Elements," which was a compilation of..

Introduction Polynomial functions are essential mathematical tools for solving real-world problems, from calculating the trajectory of a ball in flight to modeling the growth of a population. The study of polynomial functions and their properties offers a rich and diverse landscape to explore, from the basic definitions to the complex applications. This report aims to provide a comprehensive gui..

Complex numbers are a fascinating and enigmatic branch of mathematics that have been captivating mathematicians for centuries. Despite their apparent simplicity, these numbers hold a wealth of properties, theorems, and applications that can be used to unlock a deeper understanding of the world around us. In this comprehensive guide, we will delve into the depths of the complex plane, exploring i..

Polynomials are one of the most fundamental concepts in mathematics and are at the heart of algebraic equations. This document delves deep into the art of factoring polynomials, exploring all of its nuances, theorems, and applications. Whether you are an expert in the field or just a curious learner, the information presented here is sure to deepen your understanding of this fascinating subject...

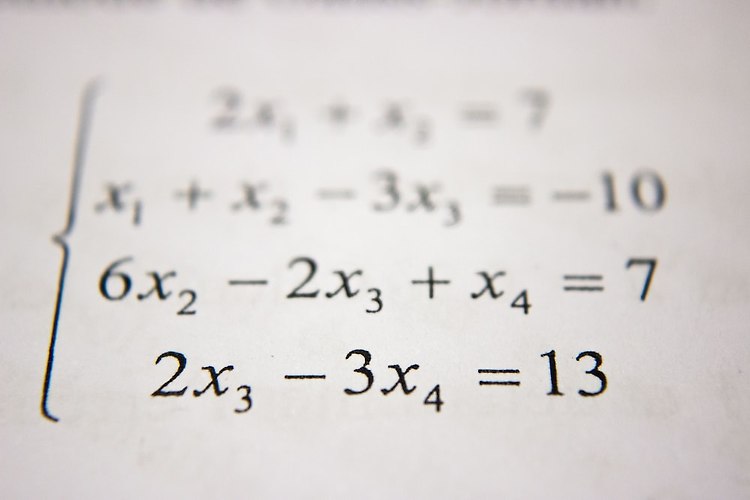
The universe is full of mysteries, but some of the most intriguing are the ones that can be solved with mathematical precision. Quadratic equations, with their parabolic curves and elegant solutions, are a prime example of this. Whether you are a student, teacher, or researcher, understanding the intricacies of quadratic equations is essential to unlocking their secrets and discovering new appli..