답이 3개인 미해결 확률 문제

 

 

확률을 잘 아시나요?

교과서에 나오는 발생빈도주의적 확률로 보았을 때

확률은 전 사건의 경우의 수 분의 해당사건이 일어날 경우의 수로 정의합니다.

이를 확장해서 기하학적 확률을 정의할 수 있는데

기하학적 확률은 전 영역의 크기 분의 특정 영역의 크기로 정의합니다.

 

 

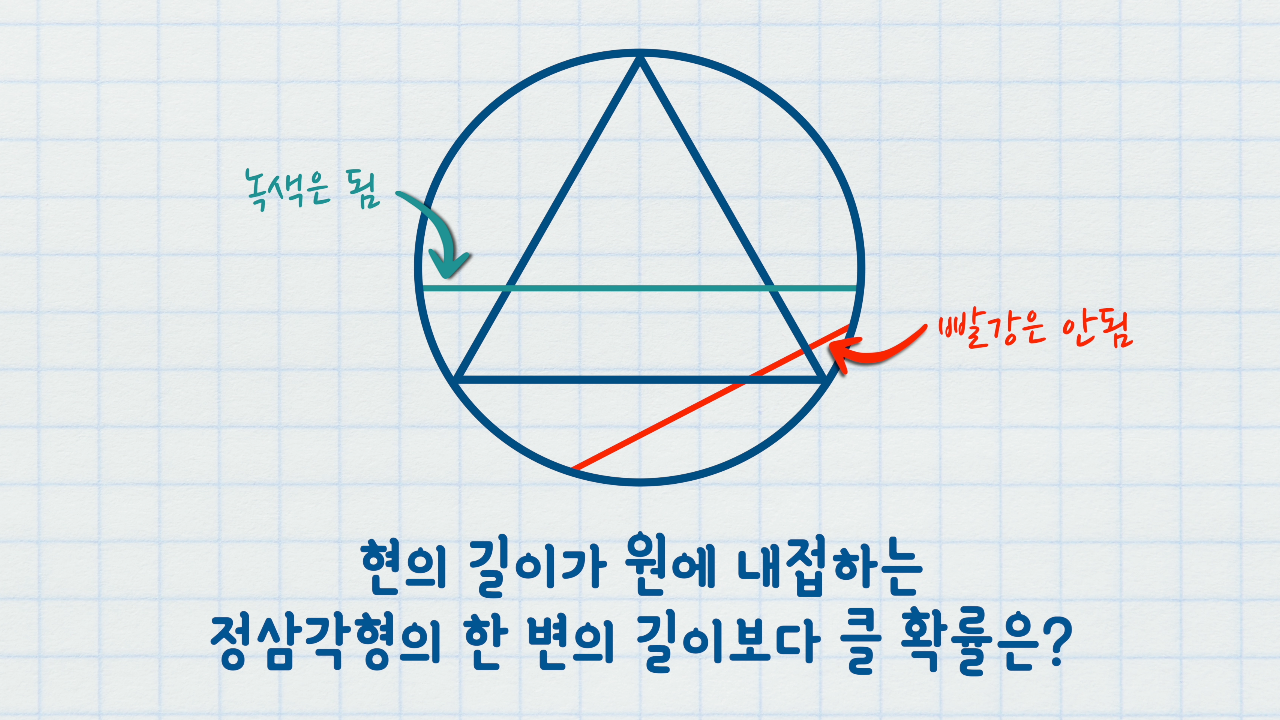
그렇다면 원에 내접하는 정삼각형, 그리고 임의의 현을 그릴 때,

현의 길이가 원에 내접하는 정삼각형의 한 변의 길이보다 클 확률을 구할 수 있을까요?

 

 

이 문제를 해결하는 3가지 방법에 대해 소개하겠습니다.

 

첫번째는 Random Endpoint 해법입니다.

현의 시작점을 삼각형의 한 꼭짓점으로 두면 현이 삼각형의 한변 보다 길어지기 위해서는 시작점의 반대쪽에 있는 변을 지나야 합니다. 따라서 현을 정의할 수 있는 각도인 180도 중 정삼각형의 한 각의 크기보다 작은 곳에서 현이 한 변의 길이보다 크므로 확률은 60/180 즉 1/3이 됩니다.

 

두번째는 Random radius해법입니다.

삼각형의 한 변과 평행한 현을 생각하면 현이 삼각형의 한 변보다 안쪽에 있어야 현이 변보다 길어질 수 있습니다. 이때 원의 내접 정삼각형의 변은 원의 반지름을 이등분하므로 확률은 1/2이 됩니다. 

 

세번째는 Random midpoint해법입니다.

삼각형에 내접하는 원을 그리면 현의 중점이 작은 원 안쪽에 놓일 경우에만 현이 삼각형의 한 변의 길이보다 크므로 전체 원의 크기 분의 작은 원의 크기를 구하면 넓이는 반지름의 크기의 제곱이므로 확률은 1/4이 됩니다.

 

 

풀이 방법에 대해 확률이 바뀌는 이 문제는 베르트랑의 현 Bertrand의 현이라고 불리는 패러독스입니다. 수학적으로 확률의 고전적 정의로만 본다면 셋 다 정답이 됩니다. 그렇다면 현실에서도 그럴까요?

 

현실세계에서는 신기하게도 Random radius해법만 성립합니다. 현실세계에서는 중력이 작용하면서 Random radius해법만이 통계역학이나 가스 물리학, 고전역학으로 확률을 구하는 실험에서 특정 물리적 시스템에 존재하는 변형 불변량을 충족시키는 유일한 솔루션이 되기때문입니다. 다른말로 Random Endpoint 해법과 Random midpoint해법은 수학적으로는 존재하나 우리가 사는 세상에서는 존재할 수 없는 확률인거죠. 현재까지도 수학에서는 이 문제에 대한 논의가진행 중입니다. 컴퓨터 시뮬레이션 등 여러가지 방법으로 접근해도 확률의 고전적 정의에 대한 명확한 오류를 찾지 못했습니다. 그래서 이 세가지 풀이를 모두 인정하고 있는데, 여러분들은 어떻게 생각하시나요? 수학에서 답이 3개인 문제 자명하신가요?

 

 

 

빈도주의는 직접 시행할 수 있는 사건만이 확률이라고 봅니다. 즉, 통계적 확률이야 말로 진짜 확률이며, 시행을 무한히 할 수 있을 때야 말로 정확한 확률을 계산할 수 있다고 생각했습니다. 빈도주의와 고전적 확률 모두 객관적인 입장에서 확률을 정의하며 확률의 정의에 반복적인 시행이 요구되기 때문에, 시행의 횟수가 한계적이거나, 미래의 일어나지 않는 사건의 정확한 확률을 정의할 수 없습니다. 빈도주의 학파의 관점에서 베르트랑 역설은 정의될 수 없습니다. 해법들 중 하나를 선택해야만 실제로 시행할 수 있으므로 문제가 해결되는거죠.

베이즈 주의는 모든 확률은 불안정하며, 확률은 믿음의 정도로 해석한다고 봅니다. 베이즈 확률에서는 불안정한 사전 확률이 존재하며, 여기에 보다 정확한 확률을 위해 증거를 사용하여 해당 확률을 보완합니다. 여기에는 그 증거가 관찰될 확률, 즉 우도(Likelihood)만 알면됩니다. 이렇게 갱신된 사후 확률 (Posterior Probability)은 이전보다 정확하다고 판단하며, 추후에 다시 새로운 증거를 확보하여 갱신하는 것으로 완벽한 확률에 근사합니다.

베이즈 주의는 주관적인 입장에서 확률을 정의하며 베이즈 주의의 확률은 사용되는 증거에 따라 다른 양상을 보이고 하나의 특정한 확률이 정답이라기 보다는 그냥 다수가 인정하는 확률을 당장은 정답이라고 보는 편입니다. 빈도주의와 달리, 시행의 횟수가 한계적이거나, 미래의 일어나지 않은 사건에 대해서도 주관적인 확률을 얻을 수 있어우리가 시행하는 통계조사의 기틀을 마련합니다. 예를들어 제가 대통령이 될 확률은 고전적 정의로 1/5000만이지만 실제로 전 대통령 할 생각도 다른 사람들이 뽑아줄리도 없으니 확률은 더 낮게 책정되야하는 것이죠.