폴리아 추측

수학에서는 끊임없는 탐구와 질문이 이어지곤 합니다. 그리고 그 탐구의 발판이 되는 것이 바로 추측입니다. 추측은 어떤 수학적 성질이 일정한 범위 또는 특정 조건에서 참이라고 생각되지만 아직 증명되지 않은 주장입니다.

 

예를 들어 골드바흐의 추측이 있죠. 골드바흐의 추측은 수학의 유명한 미해결 문제 중 하나로, 독일의 수학자 크리스티안 골드바흐(Christian Goldbach) 가 1742년에 처음 제시했습니다. 이 추측은 간단하면서도 아름답게 표현됩니다.

 

($4$보다 크거나 같은) 모든 짝수는 두 소수의 합으로 표현할 수 있다.

 

쉽게말해 어떤 짝수 $n$이 주어졌을 때, 두 소수 $p$와 $q$가 존재하여 $n=p+q$입니다. 예를 들어, 다음과 같은 조합 등이 있습니다.

 

$$4=2+2,6=3+3,8=3+5$$

 

이러한 조합은 꽤 큰 수에서도 잘 맞아 떨어집니다.

 

$$\begin{array}{rl}10& =3+7\\ 100& =47+53\\ 1000& =491+509\\ 10000& =4649+5351\\ 100000& =49877+50123\end{array}$$

1938년 닐스 피핑(Nils Pipping)은 수작업으로 $n=100,000$인 경우까지 검증했습니다. 그 후 컴퓨터의 도움을 받아, 더 많은 수들에 대해 진위가 확인되었습니다. 특히, T. Oliveira e Silva는 분산 컴퓨팅 검색을 수행하여 $n\le 4\times {10}^{18}$ ($400$경, $4\times {10}^{17}$까지는 두 번 검증)까지 이 추측을 검증했습니다. 이는 작은 모래알을 나열해서 지구를 $1$억 번 정도 돌 수 있는 길이가 될 정도로 큰 수입니다.

 

모래알 한 개의 길이는 $1\times {10}^{-3}\mathrm{m}$라 가정하고, $4\times {10}^{18}$개의 모래알을 나열하면
$$4\times {10}^{18}\times 1\times {10}^{-3}\mathrm{m}=4\times {10}^{15}\mathrm{m}$$
지구의 둘레는 약 $4.0075\times {10}^7\mathrm{m}$이므로
$$\frac{4\times {10}^{15}\mathrm{m}}{4.0075\times {10}^7\mathrm{m}}=\frac{4}{4.0075}\times {10}^8\approx 100\times {10}^6$$

 

골드바흐의 추측은 수백 년 동안 수많은 수학자들에게 도전의 기회를 제공했으며, 많은 짝수에 대해 실험적으로 검증되었습니다. 그렇다면 이렇게 큰 수까지 증명되면 참이라고 할 수 있을까요?

 

폴리아 추측(Pólya conjecture)

폴리아 추측은 조지 폴리아(George Pólya)가 1919년에 제시한 수학적 가설로, 소수론과 관련이 깊은 내용입니다. 이 추측은 자연수를 소인수의 개수에 따라 두 그룹으로 나누는 방식과 관련이 있습니다. 구체적으로, 폴리아 추측은 어떤 자연수 $n$에 대하여, $1$보다 크고 $n$ 이하인 모든 자연수를 소인수의 개수가 홀수인 그룹과 짝수인 그룹으로 나눌 때, 홀수인 그룹의 원소 수가 짝수인 그룹의 원소 수보다 많거나 같다고 주장합니다.

 

$$\begin{array}{|ccccc|}\hline n& \text{Prime Factorization}& \text{Classification}& \text{Odd}& \text{Even}\\ 2& 2& \text{Odd}& 1& 0\\ 3& 3& \text{Odd}& 2& 0\\ 4& 2^2& \text{Even}& 2& 1\\ 5& 5& \text{Odd}& 3& 1\\ 6& 2\times 3& \text{Even}& 3& 2\\ 7& 7& \text{Odd}& 4& 2\\ 8& 2^3& \text{Odd}& 5& 2\\ 9& 3^2& \text{Even}& 5& 3\\ 10& 2\times 5& \text{Even}& 5& 4\\ 11& 11& \text{Odd}& 6& 4\\ 12& 2^2\times 3& \text{Odd}& 7& 4\\ 13& 13& \text{Odd}& 8& 4\\ 14& 2\times 7& \text{Even}& 8& 5\\ 15& 3\times 5& \text{Even}& 8& 6\\ 16& 2^4& \text{Even}& 8& 7\\ 17& 17& \text{Odd}& 9& 7\\ 18& 2\times 3^2& \text{Odd}& 10& 7\\ 19& 19& \text{Odd}& 11& 7\\ 20& 2^2\times 5& \text{Odd}& 12& 7\\ \hline\end{array}$$

 

자세히 보도록 하겠습니다. 예를들어 $n=10$일 경우, $1$과 $10$ 사이에 있는 숫자 중 홀수 개의 소인수를 가진 수는 $2,3,5,7,8$이며, 짝수 개의 소인수를 가진 수는 $4,6,9,10$입니다. 여기서 주의하실 점은 $8$과 같이 $2\times 2\times 2$처럼 거듭 제곱인 경우 각 소인수의 성분을 세므로 $3$개의 소인수를 가진다고 봐야합니다. 이렇게 소인수 분해하고 난 후 개수를 세서 다음 표와 같이 누적해서 보면 소인수가 홀수개인 수의 개수가 짝수개인 수의 개수보다 항상 큰 것을 볼 수 있습니다.

 

앞서 본 표에서 규칙성을 보면 소수들은 홀수개의 성분으로 소인수 분해되고, 짝수개의 성분으로 소인수분해 되는 수와 홀수개의 성분으로 소인수분해 되는 수들의 개수가 앞으로도 비슷하다고 생각한다면 더 큰 수들도 조사해보았을 때 홀수개의 성분으로 소인수 분해되는 수가 항상 더 많을 것이라 생각할 수도 있습니다.

 

이 추측은 리우빌 함수(Liouville function) $\lambda (n)$을 이용해 보다 쉽게 나타낼 수 있습니다. 리우빌 함수는 자연수 $n$에 대해 정의된 함수로, $\mathrm{\Omega }(n)$을 $n$을 소인수분해한 결과에서 소인수 지수의 총합이라 할 때, 짝수이면 $+1$을, 홀수이면 $-1$을 값으로 갖는 함수입니다.

 

$$\lambda (n)=(-1{)}^{\mathrm{\Omega }(n)}$$

 

따라서 폴리아 추측은 다음과 같이 정의된 $L(x)$가 항상 $0$ 이하라는 추측입니다.

 

$$L(x)=\sum _{n\le x}\lambda (n)\le 0$$

 

모든 정수는 소수들의 곱으로 유일하게 표현될 수 있으며, 리우빌 함수는 이 소수들의 거듭제곱 지수를 통해 값을 결정하기 때문에, 서로소인 두 수의 소인수분해는 서로 영향을 주지 않아, 이들의 리우빌 함수 값의 곱은 각각의 리우빌 함수 값과 동일합니다. 따라서 리우빌 함수는 서로소인 두 정수 $a$와 $b$에 대해 $\lambda (ab)=\lambda (a)\lambda (b)$을 만족하는 곱셈적 함수이므로 이 문제의 분석을 더 간편하게 할 수 있습니다.

 

두 서로소인 양의 정수 $a$와 $b$에 대하여 $a$와 $b$가 공통된 소인수를 가지지 않으므로, $\mathrm{\Omega }(ab)$는 $\mathrm{\Omega }(a)$와 $\mathrm{\Omega }(b)$의 합과 같다.
$$\mathrm{\Omega }(ab)=\mathrm{\Omega }(a)+\mathrm{\Omega }(b)$$
리우빌 함수의 정의에 따라
$$\lambda (ab)=(-1{)}^{\mathrm{\Omega }(ab)}=(-1{)}^{\mathrm{\Omega }(a)+\mathrm{\Omega }(b)}$$
이고, 지수 법칙을 이용해 정리하면
$$(-1{)}^{\mathrm{\Omega }(a)+\mathrm{\Omega }(b)}=(-1{)}^{\mathrm{\Omega }(a)}\cdot (-1{)}^{\mathrm{\Omega }(b)}$$
다음과 같다.
$$\lambda (ab)=\lambda (a)\cdot \lambda (b)$$

 

이를 이용해 python코드를 작성하여 간단하게 $100$만 자리까지 확인해보았을 때, 비록 $L(48512)$에서 $-3$까지 영점에 근접하며 추측을 위협하지만 결국엔 수가 커져갈 수록 다시 $0$과 멀어지는 추세를 확인할 수 있습니다. 그렇다면 이 추측은 더 큰 수에서도 항상 성립한다고 할 수 있을까요?

 

쏟아지는 반례들

1958년 해즐그로브(C. B. Haselgrove)는 자신의 논문에서 폴리아의 추측이 $x<250,000$에 대해 참임을 확인했습니다. 더하여 이 추측이 항상 참이 아님도 증명합니다. 그의 증명은 리만 가설(Riemann hypothesis)을 가정하고, 리만 제타함수와 리우빌 함수와의 관계를 이용해 리만 제타 함수의 특정 값들을 분석하여 폴리아의 추측이 잘못되었음을 보여주었습니다.

 

$$\frac{\zeta (2s)}{\zeta (s)}=\sum _{n=1}^{\mathrm{\infty }}\lambda (n)n^{-s}$$

 

리만 가설에서 영점들이 $s=\frac{1}{2}+it$ 일직선상에 있다는 단순성을 가정한 잉엄(A. E. Ingham)의 작업을 인용하여 함수를 정의하고 이로부터 어떤 값$u$에 대해 $L(e^u)>0$임을 보였죠. 이후 컴퓨터를 사용하여 $\zeta (s)$를 큰 범위에서 계산했으며, 약 $1.847\times {10}^{361}$ 정도의 수에서 반례가 존재할 것으로 추정했습니다.[^1] 관측 가능한 우주에 있는 원자수가 대략 ${10}^{80}$개라고 추측하는데 해즐그로브가 추측한 반례는 우주에 있는 원자의 수를 네 제곱한 수 보다 크므로 상상도 하기 어려운 숫자죠. 그래서 구체적인 반례는 영영 확인할 수 없을 줄 알았습니다. 하지만 다행히도 추측이 거짓임이 밝혀진지 2년 뒤에 레먼(R. Sherman Lehman)은 다음 공식을 이용해 $n=906,180,359$에서 이 추측이 성립하지 않음을 보이며 처음으로 명시적인 반례를 찾아냅니다.[^2]

 

$$L(x)=\sum _{k\le g}M\left(\frac{x}{k^2}\right)+\sum _{l\le \frac{x}{g^2}}\mu (l)\lfloor \sqrt{\frac{x}{l}}\rfloor -M\left(\frac{x}{g^2}\right)\lfloor \frac{\sqrt{x}}{g^2}\rfloor$$

 

 

In the present paper we shall describe calculations which lead to the result that $L(906,180,359)=+1$. We have not found a smaller value of $x$ for which the conjecture fails, but also we have not proved that this is the smallest $x$ greater than $2$ for which $L(x)$ is positive

본 논문에서 우리는 $L(906,180,359)=+1$이라는 결과로 이어지는 계산을 설명할 것입니다. 우리는 추측이 실패하는 더 작은 $x$ 값을 찾지 못했으며, $L(x)$가 양수인 $2$보다 큰 가장 작은 $x$가 이것임을 증명하지도 못했습니다.

이후 1980년에 이르러 타나카(Minoru Tanaka)가 $n=906,150,257$이 폴리아 추측의 가장 작은 반례임을 밝혀내게 됩니다. 저도 이 문제를 직접 풀어보기위해 코드를 작성하고 이틀 간 검증해본 결과, $L(x)$의 값을 모아놓은 파일 크기만 $7\mathrm{G}\mathrm{B}$를 넘어갔지만 결국 같은 값을 구해냈습니다. 그리고 $10$억까지의 수 중에서는 $L(906,316,571)=828$이 최댓값임을 확인 했습니다. 이 결과에 대해 관심이 있으신 분들은 블로그를 참고해주시기 바랍니다.

 

 

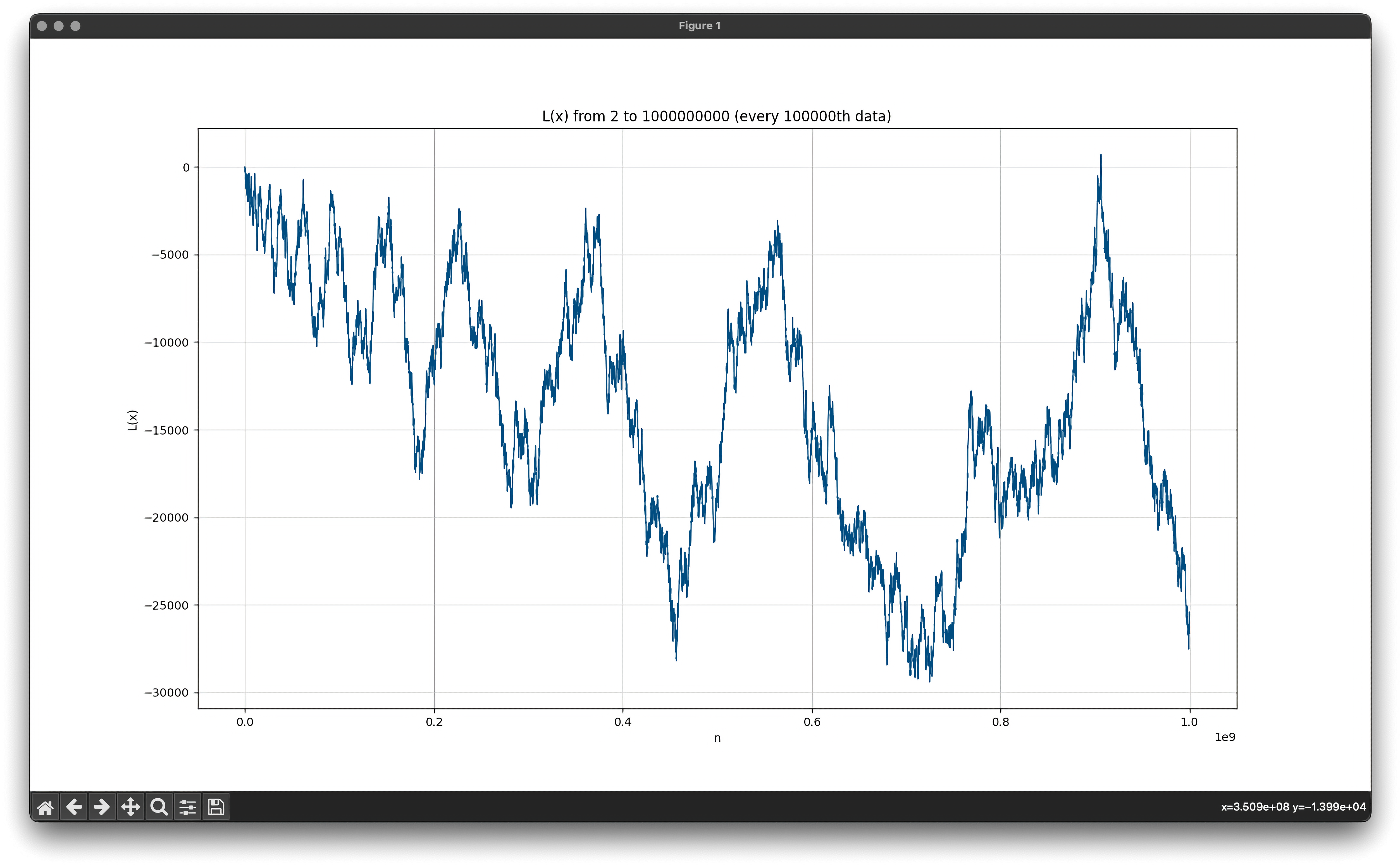
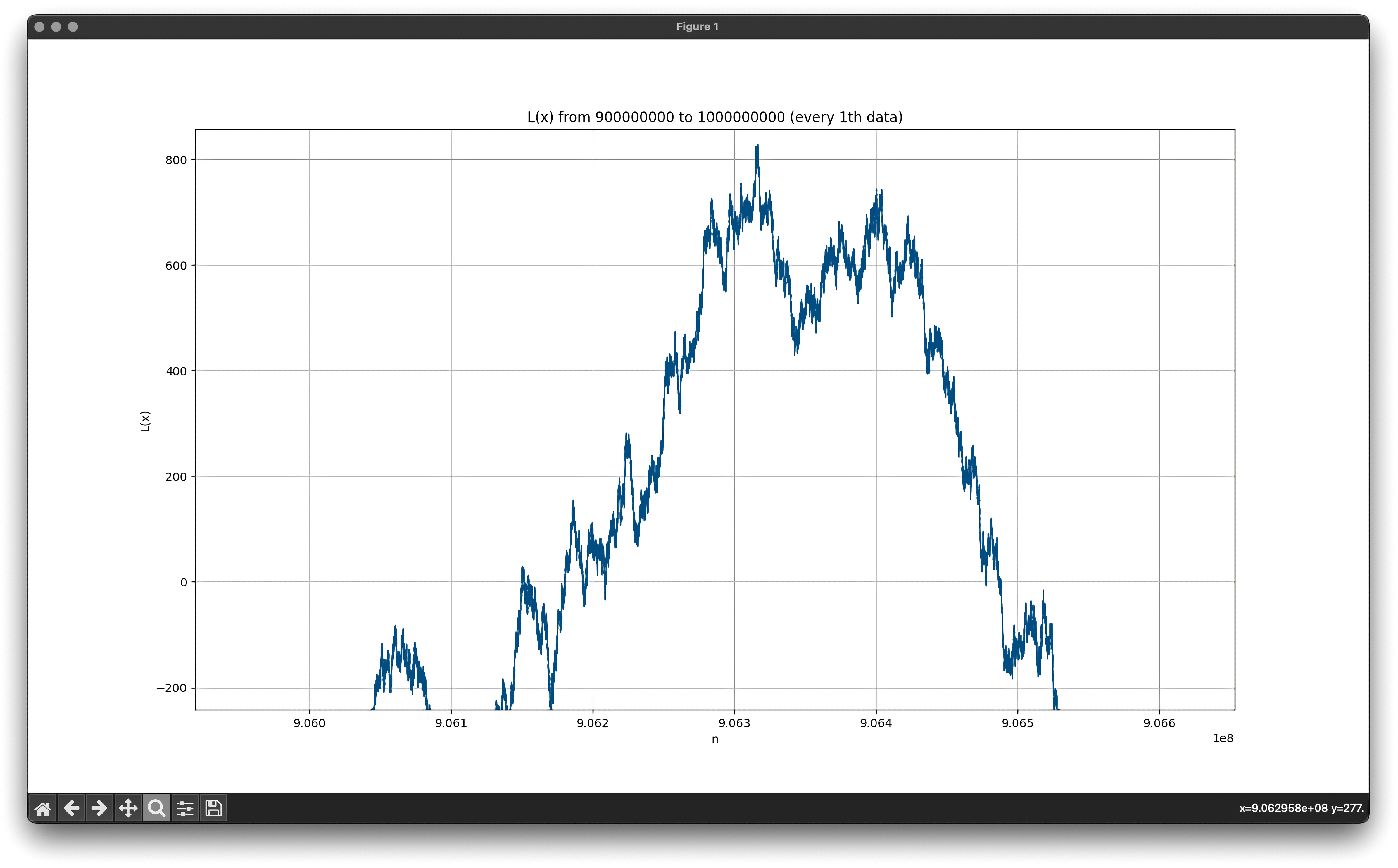
여러 연구 결과를 통해 $L(x)$가 항상 음수가 아니라 양수일 수도 있음이 밝혀졌고, 이를 만족하는 최소의 반례도 찾아냈습니다. 하지만 $L(x)$가 무한히 양수와 음수를 오가는지는 아직 열린 문제로 남겨졌습니다.[^3]

 

$10$억까지의 수 중 $L(x)=0$을 만족하는 $251$개의 $x$목록

$$\begin{array}{c}906150256,906150290,906150292,906150294,906150304,906150306,\\ 906150310,906150312,906150314,906150322,906150324,906151514,\\ 906151516,906151528,906151574,906154582,906154584,906154604,\\ 906154608,906154610,906154614,906154756,906154762,906154768,\\ 906154788,906154790,906154792,906154824,906154828,906154836,\\ 906154856,906154864,906154866,906154878,906154880,906154884,\\ 906154886,906154888,906154890,906154892,906154894,906154906,\\ 906154908,906154910,906154914,906154916,906154920,906154922,\\ 906154924,906154926,906154946,906154948,906180358,906180360,\\ 906180362,906180364,906180366,906180368,906180370,906180372,\\ 906180374,906180390,906180392,906180422,906180424,906180516,\\ 906180518,906180524,906180528,906180532,906180536,906180552,\\ 906180554,906192696,906192846,906192864,906192866,906192902,\\ 906192904,906192906,906192962,906192964,906192970,906192978,\\ 906192980,906192982,906192984,906192990,906193212,906193226,\\ 906193228,906193232,906193244,906193246,906193302,906193418,\\ 906193464,906193474,906193476,906194930,906194932,906194936,\\ 906194944,906194948,906194950,906194960,906194966,906194978,\\ 906195098,906195108,906195114,906195146,906195148,906195150,\\ 906195296,906195298,906195982,906195984,906195988,906196008,\\ 906196010,906196012,906196014,906196044,906196050,906196052,\\ 906196054,906196056,906196058,906196070,906196076,906196078,\\ 906196080,906196082,906196090,906196098,906196108,906208708,\\ 906208710,906208712,906208730,906209040,906209062,906209066,\\ 906209068,906209070,906209072,906209208,906209222,906209226,\\ 906209232,906209234,906209236,906209240,906209242,906209270,\\ 906209282,906209284,906209290,906477698,906477700,906477734,\\ 906477810,906477866,906477868,906477870,906477898,906477900,\\ 906477902,906477904,906477928,906477930,906477932,906477934,\\ 906477936,906486638,906486804,906486806,906486816,906486818,\\ 906486820,906486830,906486842,906486844,906486852,906486854,\\ 906486908,906486910,906486912,906486916,906486946,906486948,\\ 906486960,906486964,906486972,906486974,906487000,906487004,\\ 906487058,906487062,906487064,906487068,906487070,906487072,\\ 906487074,906487076,906487084,906487086,906487090,906487092,\\ 906487094,906487100,906487184,906487186,906487188,906487190,\\ 906487192,906487194,906487202,906487204,906487258,906487260,\\ 906487262,906487270,906487272,906487278,906487286,906487932,\\ 906487936,906487948,906487972,906487974,906487988,906487990,\\ 906487992,906487994,906488000,906488002,906488006,906488008,\\ 906488022,906488024,906488026,906488028,906488040,906488044,\\ 906488054,906488064,906488066,906488076,906488078\end{array}$$

 

추측 너머에

반례들은 진리를 향한 여정에서 중요한 이정표입니다. 폴리아의 추측이 틀렸다는 사실은 많은 경우에서의 진실성이 전체를 대변하지 않음을 보여주며, 특정 사례에서의 진실이 일반화될 수 없다는 중요한 교훈을 제시합니다. 그러나 이 추측을 통해 얻을 수 있는 것은 이러한 단순한 교훈뿐만이 아닙니다. 수학은 해답도 중요하지만 어쩌면 그 과정이 더 중요하다 생각합니다. 폴리아가 이 추측을 제시한 것은 정말 이 명제가 참이라고 생각해서 그런 것은 아니었습니다. 사실은 정반대 였죠. 폴리아는 이 명제가 참이라고 생각하지 않았습니다. 이 명제를 증명한 과정에서 보듯 이 추측의 본 목적은 리만 가설과 같은 깊은 수학적 문제에 대한 탐구를 촉진하고자 함이었습니다. 폴리아의 추측은 결코 오류를 의미하는 것이 아니라, 리만 가설이라는 미지의 세계로 나아가는 도전의 초대장이었습니다. 폴리아는 이 문제를 제기하고 해결함에 있어 수학의 새로운 분야를 개척할 수 있다고 생각했습니다.

 

골드바흐의 추측과 폴리아의 문제는 모두 수학 탐구의 본질을 반영합니다. 수학의 발전은 귀납적 추론을 통한 문제 발견과 연역적 과정을 통한 증명의 순환 속에서 이루어집니다. 수학은 끊임없는 탐구와 물음, 그리고 불확실성 속에서도 지식의 빛을 발견하는 여정입니다. 아직 해결되지 않은 추측은 아직 펼쳐지지 않은 수학의 무한한 가능성과 진리를 밝히기위한 불빛입니다. 그렇다면 여러분이 밝혀낼 다음 진리는 무엇인가요?

 

lambda(n).py

0.00MB

L(x).py

0.00MB

L(x) Graph.py

0.00MB

check.py

0.00MB

 

import csv
from sympy import factorint

def liouville_function(n):
    # 리우빌 함수는 소인수의 지수의 합이 홀수면 -1, 짝수면 +1을 반환합니다.
    return (-1)**sum(factorint(n).values())

def find_last_calculated(output_file):
    try:
        with open(output_file, 'r', newline='') as file:
            # 파일의 행 수를 세어 마지막으로 계산된 n 값을 추정합니다.
            row_count = sum(1 for row in file)
            return row_count if row_count > 0 else None
    except FileNotFoundError:
        return None

def calculate_liouville_values(start, end, output_file):
    last_calculated = find_last_calculated(output_file)
    if last_calculated is not None:
        start = last_calculated + 1

    with open(output_file, 'a', newline='') as output:
        writer = csv.writer(output)
        if last_calculated is None:
            writer.writerow(['Lambda(n)'])

        for n in range(start, end + 1):
            liouville_value = liouville_function(n)
            writer.writerow([liouville_value])

def main():
    start = 2
    end = 10**9
    output_filename = 'lambda.csv'
    calculate_liouville_values(start, end, output_filename)

if __name__ == "__main__":
    main()

 

import csv

def calculate_cumulative_sum(input_file, output_file):
    cumulative_sum = 0
    
    with open(input_file, 'r') as input_csv, open(output_file, 'w', newline='') as output_csv:
        reader = csv.reader(input_csv)
        writer = csv.writer(output_csv)
        
        header = next(reader)
        writer.writerow(['L(x)'])
        
        for row in reader:
            liouville_value = int(row[0])
            cumulative_sum += liouville_value
            writer.writerow([cumulative_sum])

def main():
    input_filename = 'lambda.csv'
    output_filename = 'L(x).csv'
    calculate_cumulative_sum(input_filename, output_filename)

if __name__ == "__main__":
    main()

 

import matplotlib.pyplot as plt
import csv
from itertools import islice


def plot_liouville_partial(filename, start, end, step=1):
    L_x_values = []
    x_indices = []

    with open(filename, "r") as csvfile:
        csvreader = csv.reader(csvfile)
        next(csvreader)

        for i, row in enumerate(islice(csvreader, start - 2, end - 1, step)):
            actual_row_number = start + i * step
            x_indices.append(actual_row_number)
            L_x_values.append(int(row[0]))

    plt.figure(figsize=(16, 9))
    plt.plot(x_indices, L_x_values, linewidth=1, color="#004D81")
    plt.title(f"L(x) from {start} to {end} (every {step}th data)")
    plt.xlabel("n")
    plt.ylabel("L(x)")
    plt.grid(True)
    plt.show()


filename = 'L(x).csv'
plot_liouville_partial(filename, 9 * 10**8, 10**9)

import os

def count_rows_in_csv(file_path):
    count = 0
    with open(file_path, 'r', encoding='utf-8') as file:
        for _ in file:
            count += 1
    return count

def count_rows_in_multiple_csv(file_list):
    row_counts = {}
    for file_path in file_list:
        row_counts[file_path] = count_rows_in_csv(file_path)
    return row_counts

file_list = ['lambda.csv', 'L(x).csv']

# 여러 파일의 행 수를 계산합니다.
row_counts = count_rows_in_multiple_csv(file_list)

# 결과 출력
for file_path, count in row_counts.items():
    print(f"{file_path}: {count}")

 

[^1]: A disproof of a conjecture of Pólya - Haselgrove - 1958
[^2]: On Liouville's Function By R. Sherman Lehman
[^3]: A Numerical Investigation on Cumulative Sum of the Liouville Function