세상을 바꾼 17가지 방정식 - 3. 미적분

 

17세기는 운동에 관한 중요한 법칙들이 발견되는 시기였습니다. 갈릴레오 갈릴레이는 물체가 자유낙하 상태에서 일정한 가속도로 움직인다는 것을 발견하였고,

$$ v=gt$$

$v$는 속도, $g$는 중력 가속도(지구에서 약 9.8 m/s²), $t$는 시간

케플러는 행성이 태양 주위를 어떻게 움직이는지를 설명했죠.

1. 제1법칙 (궤도의 법칙): 모든 행성은 태양을 한 초점으로 하는 타원 궤도를 따라 움직인다.
2. 제2법칙 (면적의 법칙): 행성이 태양과 그 사이의 선분이 그리는 면적은 일정한 시간 동안 일정하다.
3. 제3법칙 (주기의 법칙): 행성의 궤도 주기의 제곱은 그 궤도의 장반경의 세제곱에 비례한다.

갈릴레오의 운동법칙과 케플러의 행성 운동법칙은 각각 특정한 상황에서 물체의 운동을 설명했지만 이 두 법칙은 그 범위가 제한적이며, 모든 상황에서 물체의 운동을 설명할 수는 없었습니다. 이런 한계를 극복하기 위해 뉴턴은 보다 일반적인 운동법칙을 제시하게 되는데 우리가 흔히 알고 있는 뉴턴의 운동법칙입니다.

1. 제1법칙 (관성의 법칙): 외부 힘이 작용하지 않는 물체는 휴면 상태를 유지하거나, 일정한 속도로 직선 운동을 계속한다.
2. 제2법칙 (가속도의 법칙): 물체에 작용하는 힘은 물체의 질량과 가속도의 곱과 같다.
3. 제3법칙 (반작용의 법칙): 물체 A가 물체 B에 힘을 가하면, 물체 B는 물체 A에 동일한 크기의 힘을 반대 방향으로 가한다.

여기서 두 번째 법칙인 가속도의 법칙을 눈여겨 보겠습니다. 가속도의 법칙은 "물체에 작용하는 힘은 그 물체의 질량과 가속도의 곱과 같다."라고 표현합니다.

$$F=ma$$

힘은 속도가 아니라 속도의 변화량과 관련이 있다는 거죠. 여기서 반대로 이러한 질문할 수 있습니다. 이 세상에 변화하지 않는게 있을까요? 우리는 그러한 변화를 어떻게 이해하고 표현할 수 있을까요?

뉴턴과 라이프니츠의 미적분

뉴턴이 미적분학을 발명하게 된 배경은 그의 과학적인 문제 해결 과정에서 시작되었습니다. 그는 물리학적 현상, 특히 운동에 대한 자연의 법칙을 찾아내려는 노력 속에서 미적분학의 필요성을 느꼈습니다. 당시 그는 물체의 속도나 위치가 시간에 따라 어떻게 변하는지를 정확히 설명하고 계산하는 방법이 필요했지만 그런 방법은 당시에는 존재하지 않았습니다. 이런 문제를 해결하기 위해 뉴턴은 '플럭시온(fluXion)'이라는 방법을 개발하였고, 이는 나중에 우리가 지금 알고 있는 미적분학으로 발전하게 되었습니다.

반면에 라이프니츠는 사회, 철학, 언어학, 법학, 역사학, 그리고 기술까지 다양한 분야에서 지식을 탐구했습니다. 그의 연구의 주요 목표 중 하나는 모든 학문의 지식을 통합하고 이해하는 보편적인 언어와 방법론을 찾는 것이었죠. 이러한 추구가 그를 수학의 세계로 인도했고, 그는 수학이 이러한 보편적 언어가 될 수 있음을 깨달았습니다. 이 과정에서 그는 미분과 적분을 발견하게 되었고, 미적분학의 기본 이론인 '미분과 적분의 기본 정리'를 정리했습니다.

뉴턴과 라이프니츠가 동시대에 미적분을 발견하게 된 것은 사실 피에르 드 페르마의 미적분학 초기 연구 덕분입니다. 페르마는 최대 최소 문제에 대한 접근법을 통해 접선의 개념을 도입하였고, 이 접선의 개념은 뉴턴과 라이프니츠가 미적분학을 발전시키는데 중요한 역할을 하게된거죠. 우리가 교과서에서 배우듯 페르마는 곡선의 특정 지점에서의 기울기를 찾는 방법으로써 접선의 개념을 도입하였습니다. 이는 곡선 위의 한 점 주변의 작은 부분을 곧은 선으로 근사화하는 것을 의미하며, 그 지점에서의 기울기를 구하는 방법을 제공합니다. 뉴턴과 라이프니츠는 페르마의 이 접선 개념을 받아들이고 확장하였습니다. 뉴턴은 '플럭시온' 이론을 개발하였고, 라이프니츠는 '차분' 방법론을 제안하였습니다. 이들 방법론은 모두 곡선의 점에서의 기울기를 계산하려는 페르마의 원래 접근법을 수학적으로 엄밀하게 만든 결과인거죠.

뉴턴의 플럭시온

플럭시온(fluxions)은 아이작 뉴턴이 개발한 수학적 방법으로, 현대의 미분법에 대응되는 개념입니다. 뉴턴은 Fluxion을 어떤 양 $x$ (Fluent라고 불림)의 속도로 정의하고,Fluxion을 변화하는 양의 순간적인 속도 즉, 변화율로 보았습니다. 뉴턴은 Fluent가 "무한히 작은" 시간 $o$ 동안 증가하는 양을 순간이라고 정의했습니다. 따라서 $x$의 순간은 $x + \dot x\cdot o$가 됩니다. 이 뜻은 어떤 방정식이 시간에 따라 변하지 않는 Fluent 인 $x$와 $y$의 관계를 표현한다면 그 방정식은 $x + \dot x\cdot o$와 $y + \dot y\cdot o$관계로 확장 될 수 있다는 것을 의미합니다.

우선 쉬운 예를 들어 뉴턴의 미분을 설명해보겠습니다. $y=x^2$에 대해 $x$가 $x+o$로 증가할 때 즉, 무한소라는 $o$ 만큼의 짧은 시간 동안의 평균 변화율은 다음과 같이 적을 수 있습니다.

$$ { {(x+o)^2-x^2 \over o} } = {{2xo+o^2} \over {o} } = 2x+o$$

이때 $o$는 어떤 수인지는 모릅니다. 다만 $2x+o$라는 변화율은 $o$가 무한소이므로 $0$에 한 없이 가까운 수이기에 변화율은 $2x$에 한 없이 가까울 것입니다. 결론적으로 $o$가 어떤 값인지 몰라도 순간 변화율인 $2x$를 구할 수 있는거죠.

나아가 $y=x^2$에 대해 $x$와 $y$대신 $x + \dot x\cdot o$와 $y + \dot y\cdot o$를 대입해 정리해보겠습니다.

$$y=x^2$$

이므로 $x$와 $y$대신 $x + \dot x\cdot o$와 $y + \dot y\cdot o$를 대입하면

$$y + \dot y\cdot o=(x + \dot x\cdot o)^2$$

입니다. 제곱하여 식을 정리하면

$$y + \dot y\cdot o= x^2 + 2 \dot x\cdot o +o^2$$

입니다. 이때, $y=x^2$이므로 소거하고, 무한소 $o$로 나누어주면

$$\dot y=2x \dot x +o$$

이고, $o$는 무한소이므로

$$\dot y=2x \dot x$$

라는 식을 얻을 수 있습니다. 오늘날에 $\dot y$라는 표현은 $y'$이라는 표현으로 바뀌었습니다.

라이프니츠의 dy/dx

라이프니츠의 미분법도 큰 차이는 없습니다. 다만 무한소를 $o$대신 $dx$라는 표현으로 바꾼 것 뿐이죠. $x$의 작은 변화량을 $dx$라고 하고, 원래의 공식에 $x+dx$, $y+dy$를 대입합니다.

$$\begin{align}
y+dy &=(x+dx)^2\
y+dy &=x^2+2x\cdot dx+(dx)^2\
dy &=2x\cdot dx + (dx)^2\
&\Rightarrow{{dy}\over{dx}} = 2x +dx \
&\Rightarrow {{dy}\over{dx}} = 2x
\end{align}$$

이렇게 보면 두 방식은 표기하는 방법만 다를 뿐 같은 연산이고, 그 아이디어마저도 같기에 누가 먼저 미적분을 발견했는가에 대한 논쟁이 있을 수 밖에 없습니다. 어떻게보면 초기 아이디어가 접선을 구한다는 페르마의 아이디어에서 부터 출발했기에 당연한 결과라고 생각합니다.

그런데 이 증명과정들은 모두 논리적 허점을 갖고 있습니다. 무한소는 그 자체로 정의하기 어려운 개념입니다. '아주 작은 양', '더 이상 나눌 수 없는 양'이라는 직관적인 설명 외에 구체적인 수치로 표현하기가 어렵죠. 앞서 설명에서 보면 $o$나 $dx$는 $0$이 아닌 것처럼 연산하다가 $0$처럼 취급하는 것은 논리적으로 납득하기 어렵습니다. 이런식의 연산은 $1 \times 0 = 2\times0$이므로 $1=2$라고 하는 것과 같습니다. 이로 인해 무한소를 사용한 초기의 미적분학은 비판의 대상이 되었습니다. 하지만 이 아이디어를 사용해 뉴턴은 다양한 과학적 사실을 합리적으로 설명해나아갔습니다. 100년 뒤에 코시와 바이어스트라스 등의 수학자들에 의해 무한소의 엄밀한 기초가 마련되었고, 현대에는 없어서는 안될 중요한 개념으로 자리매김했습니다.

프린키피아

라이프니츠 입장에서는 조금 억울한 측면이 있습니다. 앞서 말했듯 이 시기는 미분에 대한 개념이 싹띄우기 시작한 때라 학자들이라면 이 개념에 대해 어렴풋이 다 알고있었죠. 심지어 라이프니츠는 이 개념을 식으로 정리하고 논문을 발표한 반면 뉴턴은 그렇지 않았습니다. 그럼에도 불구하고 미적분의 창시자라 하면 뉴턴으로 알려진 이유는 프린키피아 라는 책 때문입니다. 프린키피아에는 직접적으로 미적분을 식으로 표현하지 않았지만 여러 기하학적 개념은 기본적으로 미적분학의 원리에 근거하고 있습니다. 그렇다면 왜 프린키피아에 미적분에 대한 아이디어가 있다고 하는지 살펴보겠습니다.

Philosophiae Naturalis Principia Mathematica by Isaac Newton

Philosophiæ Naturalis Principia Mathematica

1권 1장 1번 보조정리

프린키피아의 1권 1장 1번 보조정리는 다음과 같습니다.

LEMMA I. Quantitates, ut & quantitatum rationes, quæ ad æqualitatem dato tempore constanter tendunt & eo pacto propius ad invicem accedere possunt quam pro data quavis differentia; fiunt ultimo æquales. Si negas, sit earum ultima differentia D. Ergo nequeunt propius ad æqualitatem accedere quam pro data differenti

영어가 아니라서 좀 당황스럽죠. 17세기 유럽에서 라틴어는 그 시대의 학계에서 권위 있는 언어로 간주되었습니다. 라틴어로 논문을 작성함으로써 연구의 중요성과 권위성을 강조할 수 있었고, 유럽 전역의 학자들이 서로의 연구를 읽고 이해할 수 있었죠. 그래서 프린키피아도 라틴어로 작성되었습니다.

번역하면 다음과 같습니다.

보조정리 1. 주어진 시간 동안 항상 동등성을 향해 나아가는 수량과 그 비율은, 어떤 주어진 차이보다도 더 가까워질 수 있으며, 결국 같아집니다. 만약 이를 부정한다면, 그 차이를 D라고 가정합시다. 그렇다면 주어진 차이 D보다 동등성에 더 가까워질 수 없게 됩니다. 이는 가정과 상반됩니다.

극한을 배우신 분들이나 수학을 전공한 분들이라면 이 개념은 누가봐도 극한의 개념이라고 생각하실 수 있습니다. 심지어 부정해서 증명하는 방법은 엡실론-델타 논법에서 주로 사용하는 방법이죠. 이 보조정리는 극한의 초기 개념을 반영하고 있습니다. 뉴턴은 이 보조정리를 통해 무한소와 극한에 대한 그의 생각을 표현하고 변화하는 양과 그 변화율 사이의 관계를 설명하려고 했습니다.

1권 1장 2번 보조정리

프린키피아의 1권 1장 2번 보조정리는 적분에 관한 내용입니다. 보조정리 1번을 이용해 직사각형을 사용하여 곡선 아래의 영역을 근사하고, 이 직사각형의 너비를 무한히 줄이면서 그 수를 무한대로 늘려서 곡선 아래의 정확한 면적을 구하는 과정을 설명하죠. 우리가 오늘날 보는 정적분과 급수의 관계를 떠올리게 만듭니다.

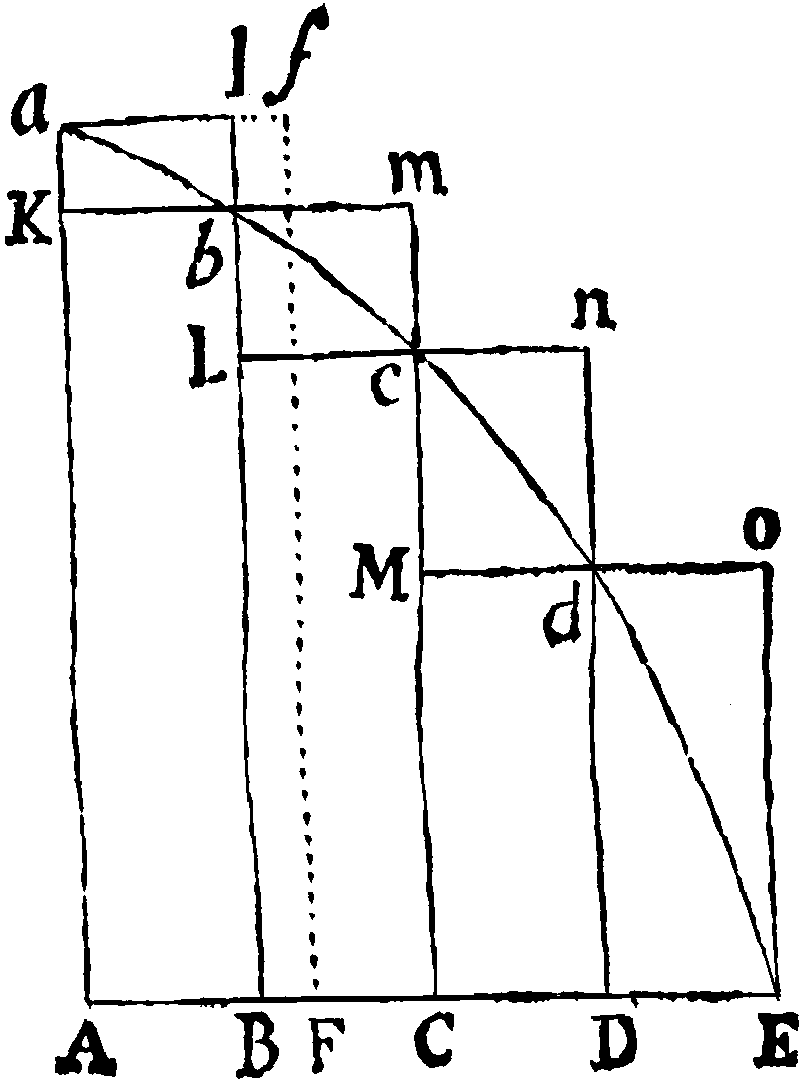
Lemma II. Si in figura quavis AacE rectis Aa, AE, & curva acE comprehensa, inscribantur parallelogramma quotcunq; Ab, Bc, Cd, &c. sub basibus AB, BC, CD, &c. æqualibus, & lateribus Bb, Cc, Dd, &c. figuræ lateri Aa parallelis contenta; & compleantur parallelogramma aKbl, bLcm, cMdn, &c. Dein horum parallelogrammorum latitudo minuatur, & numerus augeatur in infinitum: dico quod ultimæ rationes, quas habent ad se invicem figura inscripta AKbLcMdD, circumscripta AalbmcndoE, & curvilinea AabcdE, sunt rationes æqualitatis. Nam figuræ inscriptæ & circumscriptæ differentia est summa parallelogrammorum Kl + Lm + Mn + Do, hoc est (ob æquales omnium bases) rectangulum sub unius basi Kb & altitudinum summa Aa, id est rectangulum ABla. Sed hoc rectangulum, eo quod latitudo ejus AB in infinitum minuitur, sit minus quovis dato. Ergo, per Lemma I, figura inscripta & circumscripta & multo magis figura curvilinea intermedia fiunt ultimo æquales. Q. E. D.

보조정리 2. 어떤 도형 AacE에서 직선 Aa, AE 및 곡선 acE에 의해 둘러싸인 영역에, 기본선 AB, BC, CD 등이 같고, Bb, Cc, Dd 등의 도형의 변 Aa와 평행한 변을 갖는 평행사변형 Ab, Bc, Cd 등을 그릴 수 있다. 그리고 평행사변형 aKbl, bLcm, cMdn 등을 완성하십시오. 그런 다음 이 평행사변형의 너비를 줄이고 그 수를 무한대로 늘립니다. 그렇다면, 그림 AKbLcMdD, AalbmcndoE 및 곡선 AabcdE 사이의 최종 비율은 동등한 비율입니다. 그림 내부와 외부의 차이는 평행사변형 Kl + Lm + Mn + Do의 합이며, 모든 기본선이 같기 때문에, 이는 기본선 Kb와 높이 Aa의 합인 직사각형의 면적과 같습니다. 그러나 이 직사각형의 너비 AB는 무한히 작아지므로 주어진 어떤 값보다 작습니다. 따라서 보조정리 1에 따라, 내부 도형과 외부 도형, 그리고 중간의 곡선 도형은 결국 같아집니다. Q. E. D.

신기한 점은 프린키피아를 읽다보면 아이디어를 수식보다는 논리와 기하학을 이용해 주로 설명합니다. 우리가 오늘날 쓰는 극한 표현과는 사뭇 다르죠. 그 이유는 부가 정리 1권 1장 보조정리 11번의 부가설명들을 보면 좋을 것 같습니다.

Quæ de curvis lineis deq; superficiebus comprehensis demonstrata sunt, facile applicantur ad solidorum superficies curvas & contenta. Præmisi vero hæc Lemmata ut effugerem tædium deducendi perplexas demonstrationes, more veterum Geometrarum, ad absurdum. Contractiores enim redduntur demonstrationes per methodum indivisibilium. Sed quoniam durior est indivisibilium Hypothesis; & propterea Methodus illa minus Geometrica censetur, malui demonstrationes rerum sequentium ad ultimas quantitatum evanescentium summas & rationes, primasq; nascentium, id est, ad limites summarum & rationum deducere, & propterea limitum illorum demonstrationes qua potui breuitate præmittere. His enim idem præstatur quod per methodum indivisibilium, & principiis demonstratis jam tutius utemur. Proinde in sequentibus, siquando quantitates tanquam ex particulis constantes consideravero, vel si pro rectis usurpavero lineolas curvas, nolim indivisibilia sed evanescentia divisibilia, non summas & rationes partium determinatarum, sed summarum & rationum limites semper intelligi, vimq; talium demonstrationum ad methodum præcedentium Lemmatum semper revocari.

곡선과 포함된 표면에 대한 설명은 쉽게 곡선의 표면과 내용에 적용됩니다. 그러나 나는 고대 기하학자들의 방식으로 복잡한 증명을 추론하기 위한 지루함을 피하기 위해 이 보조정리를 앞서 제시했습니다. 실제로, 증명은 불가분의 방법을 통해 간결해집니다. 그러나 불가분의 가설이 더 어렵기 때문에 그 방법은 덜 기하학적으로 간주되므로, 나는 다가오는 양의 극한과 비율을 증명하고 싶었습니다. 이를 통해 불가분의 방법을 통해 동일한 것이 제공되며, 이미 증명된 원칙을 더 안전하게 사용할 수 있습니다. 따라서 다음에, 나는 양을 부분으로 구성된 것처럼 고려하거나, 곡선을 직선으로 사용하면 항상 극한을 의미하고, 그러한 증명의 힘을 앞서 제시된 보조정리의 방법으로 되돌리기를 원하지 않습니다.

원문에서 "methodum indivisibilium"은 "불가분의 방법" 또는 "불분리 방법"으로 해석될 수 있습니다. 오늘날 우리가 '무한소'라고 부르는 개념이죠. 당시 뉴턴은 미적분학의 기초 개념에 대한 근본적인 도전에 직면했습니다. 특히, 사라지는 양의 극한 비율이나 무한히 증가하는 양의 극한 비율 같은 개념은 명확하게 정의되지 않았죠. 이러한 개념들은 수학의 기초를 흔들며, 다른 사람들로 하여금 그 정당성에 대한 의문을 제기하였습니다. 뉴턴은 이러한 도전을 해결하기 위해 "프린키피아"에서 불가분의 방법을 사용하여 미적분학의 개념을 명확히 설명하려고 하였습니다. 그는 양이 사라지거나 무한히 증가할 때의 극한 비율을 정의한 것이죠. 다음 문단을 보면 이 내용에 대한 이야기가 나와 있습니다.

Objectio est, quod quantitatum evanescentium nulla sit ultima proportio; quippe quæ, antequam evanuerunt, non est ultima, ubi evanuerunt, nulla est. Sed & eodem argumento æque contendi posset nullam esse corporis ad certum locum pergentis velocitatem ultimam. Hanc enim, antequam corpus attingit locum, non esse ultimam, ubi attigit, nullam esse. Et responsio facilis est. Per velocitatem ultimam intelligi eam, qua corpus movetur neq; antequam attingit locum ultimum & motus cessat, neq; postea, sed tunc cum attingit, id est illam ipsam velocitatem quacum corpus attingit locum ultimum & quacum motus cessat. Et similiter per ultimam rationem quantitatum evanescentium intelligendam esse rationem quantitatum non antequam evanescunt, non postea, sed quacum evanescunt. Pariter & ratio prima nascentium est ratio quacum nascuntur. Et summa prima & ultima est quacum esse (vel augeri & minui) incipiunt & cessant. Extat limes quem velocitas in fine motus attingere potest, non autem transgredi. Hæc est velocitas ultima. Et par est ratio limitis quantitatum & proportionum omnium incipientium & cessantium. Cumq; hic limes sit certus & definitus, Problema est vere Geometricum eundem determinare. Geometrica vero omnia in aliis Geometricis determinandis ac demonstrandis legitime usurpantur. Contendi etiam potest, quod si dentur ultimæ quantitatum evanescentium rationes, dabuntur & ultimæ magnitudines; & sic quantitas omnis constabit ex indivisibilibus, contra quam Euclides de incommensurabilibus, in libro decimo Elementorum, demonstravit. Verum hæc Objectio falsæ innititur hypothesi. Ultimæ rationes illæ quibuscum quantitates evanescunt, revera non sunt rationes quantitatum ultimarum, sed limites ad quos quantitatum sine limite decrescentium rationes semper appropinquant, & quas propius assequi possunt quam pro data quavis differentia, nunquam vero transgredi, neq; prius attingere quam quantitates diminuuntur in infinitum. Res clarius intelligetur in infinite magnis. Si quantitates duæ quarum data est differentia augeantur in infinitum, dabitur harum ultima ratio, nimirum ratio æqualitatis, nec tamen ideo dabuntur quantitates ultimæ seu maximæ quarum ista est ratio. Igitur in sequentibus, siquando facili rerum imaginationi consulens, dixero quantitates quam minimas, vel evanescentes vel ultimas, cave intelligas quantitates magnitudine determinatas, sed cogita semper diminuendas sine limite.

반대로, 사라지는 양의 극한 비율이 없다는 것입니다. 실제로 그것들이 사라지기 전에는 극한이 아니며, 사라지면 없습니다. 그러나 같은 논리로, 특정 위치로 이동하는 몸의 극한 속도도 없다고 주장할 수 있습니다. 실제로 몸이 위치에 도달하기 전에는 극한이 아니며, 도달하면 없습니다. 그리고 대답은 쉽습니다. 극한 속도는 몸이 움직이는 속도를 의미하며, 위치에 도달하기 전이나 후가 아니라 도달할 때입니다. 마찬가지로, 사라지는 양의 극한 비율은 사라지기 전이나 후가 아니라 사라질 때의 비율로 이해해야 합니다. 마찬가지로, 첫 번째 비율은 그것들이 생길 때의 비율입니다. 그리고 첫 번째와 마지막 합계는 시작하고 멈출 때입니다. 움직임이 끝날 때 속도가 도달할 수 있는 한계가 있지만 넘어서지는 않습니다. 이것이 극한 속도입니다. 그리고 모든 시작과 끝의 양과 비율의 한계에 대한 동일한 이유가 있습니다. 이 한계는 확실하고 명확하므로, 그것을 결정하는 문제는 진정한 기하학적 문제입니다. 그러나 기하학적인 모든 것은 다른 기하학적인 것들을 결정하고 증명하는 데 합법적으로 사용됩니다. 또한 주장할 수 있습니다. 만약 사라지는 양의 극한 비율이 주어진다면, 극한 크기도 주어질 것이며, 따라서 모든 양은 불가분의 부분으로 구성될 것입니다. 이는 유클리드의 "원론" 제10권에서 비측정 가능한 것에 대해 증명한 것과는 반대입니다. 그러나 이 이의는 잘못된 가설에 기반하고 있습니다. 양이 사라질 때의 극한 비율은 실제로 마지막 양의 비율이 아니라, 무한히 감소하는 양의 비율이 항상 접근하는 한계입니다. 이 한계는 주어진 차이보다 더 가까이 접근할 수 있지만, 절대로 넘어서거나 양이 무한히 줄어들기 전에 도달할 수는 없습니다. 이것은 무한히 큰 것에서 더 명확하게 이해될 수 있습니다. 만약 두 양의 차이가 주어지고 이들이 무한히 증가한다면, 이들의 극한 비율, 즉 동등한 비율이 주어질 것입니다. 그러나 이 비율이 최대 또는 극한 크기의 양이라는 것은 아닙니다. 따라서 다음에, 만약 사물의 쉬운 상상을 위해, 나는 최소한의 양, 사라지는 양, 또는 극한 양이라고 말한다면, 항상 크기로 결정된 양을 의미하는 것이 아니라, 항상 무한히 줄어들 수 있다고 생각하십시오.

뉴턴은 사라지는 양의 극한 비율이나 무한히 증가하는 양의 극한 비율이 실제로 마지막 양의 비율이 아니라, 무한히 감소하거나 증가하는 양의 비율이 항상 접근하는 한계라고 주장하였습니다. 이 한계는 양이 무한히 줄어들거나 증가하기 전에 도달할 수 있는 값이며, 이를 통해 미적분학의 기초 개념을 명확히 한거죠. 뉴턴은 당시의 수학자들에게 익숙한 기하학적 접근 방법을 사용하여 미적분학의 중요성을 인식시키게 됩니다. 복잡한 수학적 개념들을 단순화하여 전달한 '프린키피아'는 미적분학의 본질적 도전에 대한 그의 답변이자, 미적분학에 대한 깊은 이해와 현대 과학의 기초로 구축하는 데 중요한 역할을 한 작품인거죠.

프린키피아의 원 제목은 "자연 철학의 수학적 원리"입니다. 자연 현상을 수학적으로 접근하여 설명하려고 했죠. 뉴턴의 방법론은 실험과 관찰을 통한 데이터를 기반으로 수학적 모델을 구축하는 것이었습니다. 현대 과학의 기초를 형성한거죠. 이 때문에 라이프니츠는 미분을 이용하여 거의 아무것도 하지 못한 반면 뉴턴은 자연 현상을 예측하고 설명하는 데 성공했다고 평가합니다. 다음편으로 이어집니다.