격자점을 이용한 원의 넓이 근사

## 격자점을 이용한 원의 넓이 근사

원에 내접하는 다각형과 격자점에 의해 생성되는 다각형의 넓이를 비교함으로써, 격자점의 크기가 원의 넓이$A$의 근사값에 미치는 영향을 살펴볼 수 있습니다. 예를 들어, 한 격자점이 대표하는 넓이가 $\text{cell}$이라고 할 때, 원의 내부에 위치하는 격자점들에 의해 생성되는 다각형의 넓이는 이 $\text{cell}$의 개수를 $S$라 할 때, 격자점의 크기가 줄어들면 $S$의 값이 증가하여 원의 넓이 $A$의 더 정확한 근사값을 얻을 수 있습니다. 원의 넓이를 둘러싸고 그리는 각 다각형은 격자점의 크기에 따라 달라지는데, 이 근접법은 그리드가 작아질수록 원의 넓이에 대한 근사값을 더 정밀하게 제공합니다. 따라서 격자점의 크기를 줄이면서 원의 넓이를 근사화하는 방법이 매우 유효합니다.

### 원의 넓이 추정하기
우리는 주변에서 넓이를 재야할 일이 종종 있습니다. 이런 그림을 사용하여 원의 넓이를 추정하는 방법은 수학에서 중요한 개념인 구분구적법과 연관이 있습니다. 원의 정확한 넓이는 반지름의 제곱에 원주율 $\pi$를 곱해서 $A = \pi r^2$로 계산됩니다. 그러나 격자를 사용한 근사화 방법은 이론적인 계산 없이도 원의 넓이를 추정할 수 있게 해줍니다.

원이 포함된 격자점의 넓이를 이용해 원의 넓이가 근사해봅시다.

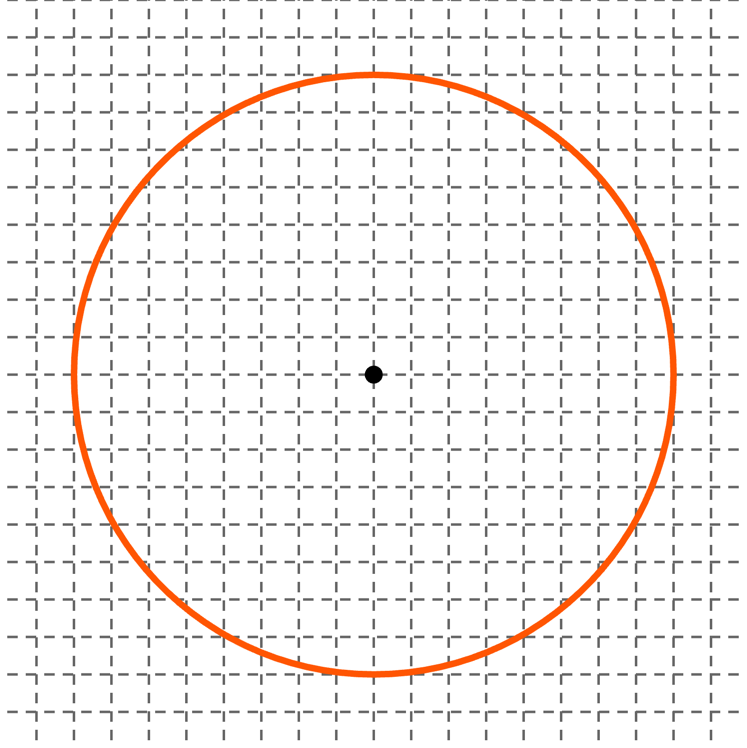
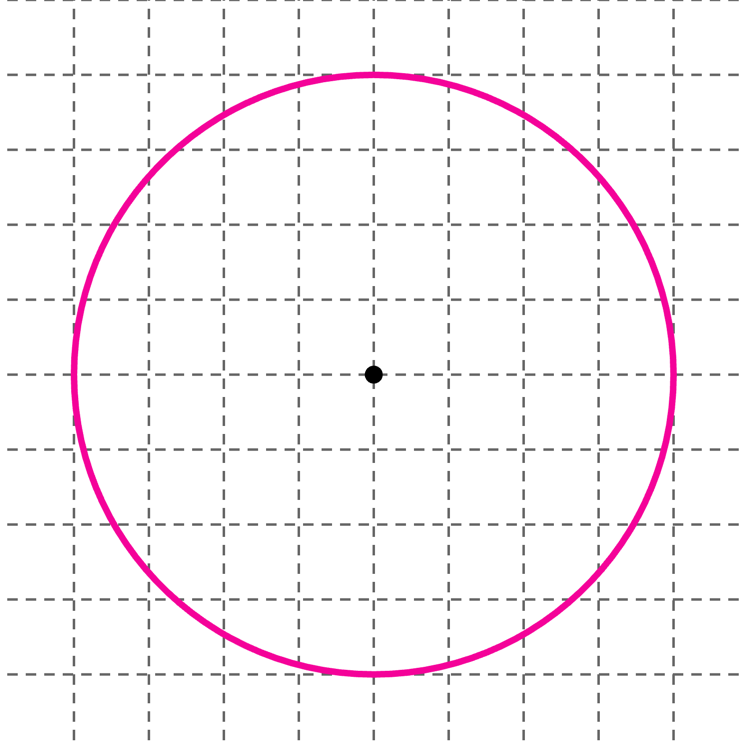
1. **격자점 세기**: 원 안에 완벽하게 들어오는 격자점의 개수를 세어보세요. 이 점들은 원의 넓이에 완전히 포함되는 부분입니다.
2. **부분 격자점 추정하기**: 원에 걸쳐 있는 격자점들도 있을 텐데요, 이 부분들은 어느 정도 넓이에 기여합니다. 이를 추정해서 세어보세요.
3. **총 격자점 계산하기**: 완전히 내접하는 격자점과 부분적으로 기여하는 격자점의 수를 합해봅시다.
5. **실제 넓이와 비교하기**: 이제 격자점 하나의 면적을 이용해 실제 원의 넓이인 $64\pi$와 비교해봅시다.

#### 질문:
- 추정한 원의 넓이와 실제 원의 넓이 사이에 어떤 차이가 있는지 알아봅시다. 차이가 있다면, 그 이유는 무엇일까요?
- 격자의 크기를 더 작게 하면 원의 넓이 추정이 더 정확해질까요?

## 원의 넓이와 극한
원의 넓이를 추정하는 고전적인 방법 중 하나는 다각형을 이용한 방법입니다. 원 안에 내접하는 정다각형의 넓이를 구하여, 이를 통해 원의 넓이를 추정하고, $\pi$의 근삿값을 구하는 것이죠. 

 

 

 

그림에서는 정6각형, 정8각형, 정16각형이 원 안에 내접하고 있는 모습을 보여줍니다. 이 다각형들의 변이 원에 접하면서, 변의 수가 증가할수록 원의 형태에 더 가까워지는 것을 알 수 있습니다. 각각의 다각형은 변의 개수가 늘어날수록 원의 넓이에 점점 더 근접하게 됩니다. 

정$n$각형의 한 변의 길이를 $A_1A_2$라 하고, 해당 변에 대한 높이(중심에서 변으로의 수선의 길이)를 $h_n$이라고 할 때, 정$n$각형의 넓이 $S_n$은 다음과 같이 계산됩니다.

$$
\begin{align*}
S_n &= \frac{1}{2} \cdot n \cdot A_1A_2 \cdot h_n \\
&= \frac{1}{2} \cdot n \cdot (\text{변의 길이}) \cdot (\text{높이})
\end{align*}
$$

이때, $n$이 매우 큰 값으로 갈수록 정$n$각형의 둘레는 원의 둘레인 $2\pi r$에 점점 가까워집니다. $h_n$ 또한 원의 반지름 $r$에 가까워지게 되죠. 따라서, $n$이 무한대로 갈수록 정$n$각형의 넓이 $S_n$은 원의 넓이인 $\pi r^2$에 접근하게 됩니다.

원의 넓이 $S$는 다음과 같이 극한을 사용하여 표현할 수 있습니다.

$$
\begin{align*}
S &= \lim_{n \to \infty} S_n \\
&= \lim_{n \to \infty} \frac{1}{2} \cdot n \cdot A_1A_2 \cdot h_n \\
&= \frac{1}{2} \cdot \lim_{n \to \infty} n \cdot A_1A_2 \cdot \lim_{n \to \infty} h_n \\
&= \frac{1}{2} \cdot 2\pi r \cdot r \\
&= \pi r^2
\end{align*}
$$

이 방법을 이용하면, 원의 넓이를 구하는 데 필요한 $\pi$의 값을 직접 계산하지 않고도, 정다각형을 통해 $\pi$의 근삿값을 구할 수 있습니다.