오일러 지표와 다면체

 

1. 오일러의 다면체 정리 개요

오일러의 다면체 정리는 수학의 기하학적인 이해를 크게 발전시킨 중요한 정리입니다. 1752년, 스위스의 유명한 수학자 레온하르트 오일러에 의해 발견된 이 정리는, 다면체를 구성하는 꼭짓점, 모서리, 면 사이의 기본적인 관계를 수학적으로 표현합니다. 이 정리는 단순하지만 강력한 공식 v - e + f = 2로 표현되며, 여기서 v는 꼭짓점의 수, e는 모서리의 수, f는 면의 수를 나타냅니다.

오일러의 다면체 정리는 수학, 특히 위상수학에서의 기본적인 개념을 형성하는 데에 큰 역할을 합니다. 이 정리는 다양한 형태의 다면체가 어떻게 구성되어 있는지 이해하는 데 필수적인 토대를 제공하며, 이로 인해 수학자들은 다면체의 복잡한 구조를 더 잘 이해할 수 있게 되었습니다. 또한, 이 정리는 다면체뿐만 아니라 다차원적인 형태와 공간에 대한 이해를 넓히는 데에도 중요한 역할을 합니다.

오일러의 다면체 정리는 수학의 여러 분야, 특히 조합론, 대수학, 기하학 등에서 중요한 위치를 차지하고 있습니다. 이 정리는 복잡한 수학적 문제를 해결하거나 새로운 수학적 이론을 개발하는 데 기초가 되며, 고급 수학 연구뿐만 아니라 중등 교육과정에서도 중요한 교육 자료로 활용됩니다. 오일러의 다면체 정리는 수학이론의 아름다움과 실용성을 모두 갖춘 대표적인 예로, 수학 분야에서의 위치와 중요성은 시간이 지남에 따라 더욱 확고해지고 있습니다

 

2. 코시의 오일러 다면체 정리 증명

이 증명은 다면체의 기하학적 특성을 활용하여, 오일러의 공식 $V - E + F = 2$를 간단하고 직관적으로 설명합니다. 다음은 코시의 증명을 각색한 자세한 설명입니다.

1단계: 다면체를 평면으로 전개하기

먼저, 다면체의 한 면을 잘라내고 나머지 면들을 평면 위에 펼쳐서 평면 지도를 만듭니다. 이때, 꼭짓점의 개수 $V$와 모서리의 개수 $E$는 변하지 않습니다. 하지만, 한 면을 제거했기 때문에 면의 개수 $F$는 1만큼 줄어들게 됩니다. 따라서, 평면 지도에서는 $V - E + F = 1$이 됩니다.

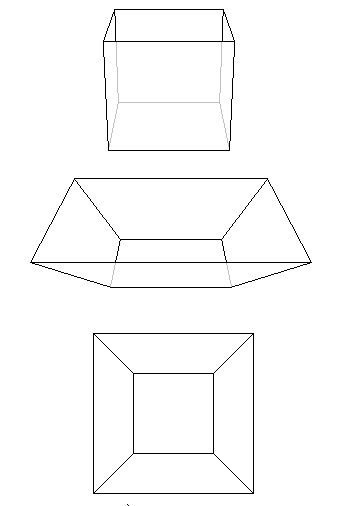
2단계: 평면 지도를 삼각형으로 분할하기

평평하게 펼쳐진 평면 지도에서, 삼각형이 아닌 다각형을 찾아 대각선을 그어 삼각형으로 만듭니다. 대각선을 그을 때마다, 모서리 $E$와 면 $F$가 각각 1씩 증가합니다. 그러나 이러한 변경은 $V - E + F = 1$이라는 관계에 영향을 주지 않습니다.

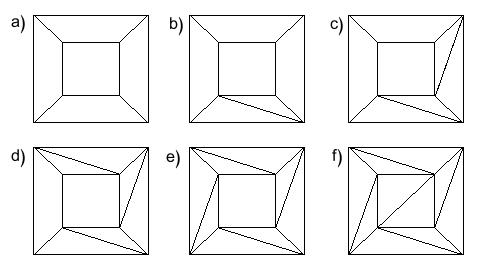
3단계: 삼각형을 하나씩 제거하기

이제 평면 지도에서 모든 면이 삼각형으로 분할되었다고 가정합니다. 삼각형을 하나 제거할 때, 모서리를 하나 제거하거나 또는 모서리 두 개와 꼭짓점 하나를 동시에 제거합니다. 이 과정에서 $V - E + F$ 값은 변하지 않습니다. 이 절차를 계속하면, 최종적으로 한 개의 삼각형만 남게 됩니다. 이 삼각형에서도 $V - E + F = 1$이 성립합니다.

코시의 증명은 기하학적 직관을 활용하여 오일러의 공식이 성립하는 이유를 명확하게 보여줍니다. 이 증명은 다면체가 어떻게 구성되어 있는지에 대한 깊은 이해를 제공하며, 위상수학 및 기하학의 기본 개념을 설명하는 데 매우 유용합니다.

 

3. 오일러 지표

오일러 지표(Euler characteristic)는 위상수학에서 폐쇄된 면을 가진 공간의 특성을 나타내는 수학적 속성입니다. 구체적으로, 오일러 지표는 꼭짓점의 개수 $V$, 모서리의 개수 $E$, 면의 개수 $F$를 사용하여 $V - E + F$로 계산됩니다. 예를 들어, 단순한 입체 도형인 정육면체(주사위)는 8개의 꼭짓점, 12개의 모서리, 6개의 면을 가지므로 오일러 지표는 $8 - 12 + 6 = 2$가 됩니다.

오일러 지표는 다양한 위상적 공간에서 일정한 값을 가지며, 이는 공간이 어떻게 변형되든 간에 변하지 않는 위상적 불변량입니다. 예를 들어, 구면(sphere)은 오일러 지표가 2인 반면, 토러스(torus)는 구멍이 하나 있어서 오일러 지표가 0입니다.

더 복잡한 곡면이나 다차원 도형에서 오일러 지표는 구멍의 수나 공간의 '손잡이'의 개수에 따라 달라질 수 있으며, 이를 통해 공간의 위상적 특성을 분류하고 이해하는 데 중요한 역할을 합니다. 예를 들어, $g$개의 구멍을 가진 면의 오일러 지표는 $2 - 2g$로 일반화될 수 있습니다.

 

4. 위상수학

오일러의 다면체 정리는 단순한 기하학적 개체인 다면체에 대한 연구에서 출발했습니다. 그러나 이 정리는 곧 기하학적 구조의 근본적인 특성을 새로운 방식으로 이해하는 데 기여했습니다.

위상수학은 공간의 연속적인 변형에 의해 변하지 않는 속성을 연구하는 수학의 한 분야입니다. 오일러의 발견은 공간이 어떻게 연결되어 있는지, 구멍이 있는지와 같은 속성이 왜 중요한지를 밝히는 데 중요한 역할을 했습니다. 이러한 연구는 고무줄이나 도넛과 같은 일상적인 물체의 형태를 고려할 때 특히 중요합니다.

오일러의 다면체 정리는 이러한 복잡한 형태의 기본적인 특성을 수학적으로 이해할 수 있는 길을 열어주었습니다. 이는 다양한 차원의 공간과 복잡한 형태를 이해하고자 하는 현대 위상수학으로 발전하는 데 필수적인 단계였습니다. 따라서, 오일러의 정리를 통한 위상수학의 발전은 우리가 주변 세계를 이해하고 설명하는 데 필수적인 기여를 한 것입니다.